Introduction
The selection of a drug dosage regimen in the absence of measured drug levels (ie., a priori drug dosing) is based on estimates of the patient's pharmacokinetic parameters adjusted for patient characteristics (ie., weight, age, sex, serum creatinine). This is also referred to as population kinetics. An example of a priori kinetics is the Hull and Sarrubi nomogram for aminoglycoside dosing.
The traditional use of measured drug levels (ie., a Posteriori drug dosing) is to estimate the patient's pharmacokinetic parameters from the measured drug levels without relying in any way on the population kinetics. An example of a Posteriori dosing is the Sawchuk and Zaske method for aminoglycoside dosing.
The Bayesian approach incorporates both sets of data for estimating the patient's pharmacokinetic parameters. It uses the a priori pharmacokinetic parameters of the population model as the starting estimate for an individual; it then adjusts these estimates based on the patient's measured drug levels, taking into consideration the variability of the population parameters and the variability of the serum level measurement. The population model is not discarded, rather it is incorporated into the estimation procedure. The serum level data is interpreted in light of both the variability of the population model the variability of the serum level measurement itself.
The appeal of the Bayesian approach is that it mimics human thinking. Before deciding what to do, our intuition first tries to foresee all the possibilities that might arise. Then, we judge how likely each is, based on both what we see and all our past experiences. Human intuition is good at judging what pieces of information are relevant to a question, but very unreliable in judging the relative cogency of different pieces of information. Bayes' theorem tells us quantitatively just how cogent every piece of information is, however it is not always able to discern whether a piece of information is relevant.
Precautions
| 1. | In general the Bayesian approach to the determination of individual drug-dosage requirements performs better than other approaches. However, outlying patients in a population (ie, those patients whose pharmacokinetic parameters lie outside of the 95th percentile of the population) may be put at risk. As is always the case, the computerized algorithms outlined below can only assist in the decision-making process and should never become a substitute for rational thought or informed judgment. |
| 2. | Although a single trough level can be evaluated with the Bayesian approach, more accurate results are obtained when both peak and trough levels are measured. |
| 3. | Non-steady-state levels are less reliable, Bayesian analysis is more accurate when using steady-state data. |
| 4. | Even a sophisticated Bayesian algorithm can not completely overcome bad data. The software engineer's cliché, "garbage in = garbage out", still applies. We must look at all "unusual" serum level data in a critical light. |
Pharmacokinetic formulas
The Bayesian approach estimates pharmacokinetic parameters (e.g., kel /CL and Vd) that will be most consistent with serum levels predicted by both the population model and the actual measured serum levels. To achieve that end, the least squares method based on the Bayesian algorithm estimates the parameters which minimize the following function:
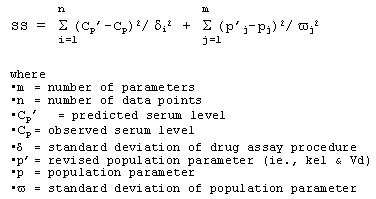
Standard deviation of population parameters
After correcting for age, weight, sex, and renal function there is a coefficient of variation of population pharmacokinetic parameters that is on the order of 20-50%. In the aminoglycoside model, 40% is used as the default value for the variability for both clearance and distribution volume. In the vancomycin model, the default variability for clearance is 40%, the default distribution volume variability is 20%. These default values may be edited on the edit drug models screen.
Standard deviation of drug assay procedure
A reasonable coefficient of variation of serum assay error is on the order of 5 to 15%. According to published data, serum assay error patterns are well represented by a second order polynomial:
SAE = SD1+ (SD2 * Cp) + (SD3 * Cp^2)
The default values used in the aminoglycoside and vancomycin models may be edited on the edit drug models screen.
Weighting of serum level data
Individual data points are then weighted according to the serum assay error (SAE), a fixed variability (SD4) which accounts for environmental errors, and the time from dose administration (Time) which gives more weight to the trough level:
Weight(i) = 1 / [ {Cp(i) * SAE + SD4} * {1.005 ^ [Interval - Time(i)] } ] ^ 2
The fixed variability value (SD4) used in the aminoglycoside and vancomycin models may be edited on the edit drug models screen.
Output assessment
The program will display the initial and final sum of residual squares (Final SS) and the number of iterations required to minimize the residual (Loop). These parameters are indicators of the accuracy of the Bayesian calculations. As a general rule, Final SS should be less than 1, and Loop should be less than 10.
Bibliography
| 1. | Sarubbi FA, Hull JW. Gentamicin serum concentrations:pharmacokinetic predictions. Ann Intern Med 1976;85:183-189. |
| 2. | Sawchuk RJ, Zaske DE, et al. Kinetic model for gentamicin dosing. Clin Pharmacol Ther 1977;21;3:362-369. |
| 3. | Peck CC, D'Argenio, Rodman JH. "Analysis of pharmacokinetic data for individualizing drug dosage regimens", in Evans W, Schentag J, Jusko J (eds): Applied Pharmacokinetics, 3rd edition. San Francisco. Applied Therapeutics, 1992; pp 3-2 to 3-26. |
| 4. | Sheiner LB, Beal S, Rosenberg B, et al: Forecasting individual pharmacokinetics. Clin Pharmacol Ther 1979;26:294. |
| 5. | Sheiner LB, Beal S. Bayesian individualization of pharmacokinetics: simple implementation and comparison with non-Bayesian methods. J Pharm Sci 1982 71:1344-1348. |
| 6. | Schumacher GE, Barr JT. Bayesian approaches in pharmacokinetic decision making. Clin Pharm 1984 3:525-30. |
| 7. | Yamaoka K, Nakagawa T, et al. A nonlinear multiple regression program based on Bayesian algorithm for microcomputers. J. Pharmacobio-Dyn., 8, 246-256 1985. |
| 8. | Ito M, Duren L, et al. Computer program for the initiation of vancomycin therapy. Clin Pharm 1993 12:126-30. |
| 9. | Burton ME, Brater DC, et al. A Bayesian feedback method of aminoglycoside dosing. Clin Pharmacol Ther 37:349-357, 1985. |
| 10. | Jelliffe R. Effect of assumptions concerning assay error patterns upon pharmacokinetic parameter values and model behavior. J. Vet Pharmacol Ther 17:105-109, 1994. |